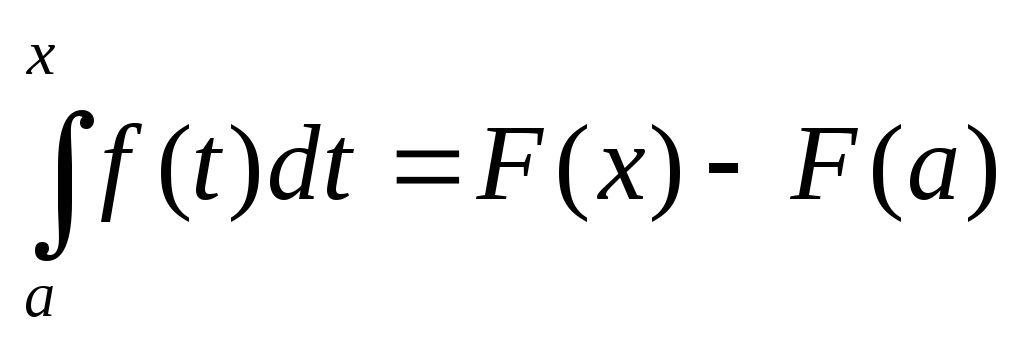Что вычисляют с помощью формулы Ньютона-Лейбница?

Узнайте, какую роль играет формула Ньютона-Лейбница в вычислении определенных интегралов. Данная формула является основной формулой интегрального исчисления и позволяет найти разность первообразных функций на отрезке [a, b]. Применение формулы Ньютона-Лейбница также рассматривается в данной статье. | NOCFN

Что вычисляют с помощью формулы Ньютона-Лейбница?

Доказательство

Пусть на отрезке [a, b] задана интегрируемая функция f.

Зададим произвольное значение x ∈ [a, b] и определим новую функцию F(x) = ∫_a^xf(t)dt. Она определена для всех значений x ∈ [a, b], потому что мы знаем, что если существует интеграл от f на [a, b], то существует также интеграл от f на [a, x], где a ≤ x ≤ b. Напомним, что мы считаем по определению F(a) = ∫_a^af(t)dt = 0 (1).

Заметим, что F(b) = ∫_a^bf(t)dt.

Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной.

Формула Ньютона-Лейбница - основная формула интегрального исчисления.

Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x), вычислить ее значения в точках a и b и найти разность F(b) – F(a).

Если после изучения данного теоретического материала (Формула Ньютона-Лейбница) у Вас возникли проблемы при решении задач на данную тему или появились вопросы образовательного характера, то Вы всегда можете задать их на нашем форуме.

Применение формулы Ньютона-Лейбница

Решение прикладных задач сводится к вычислению интеграла, но не всегда это возможно сделать точно. Иногда необходимо знать значение определенного интеграла с некоторой степенью точности, к примеру, до тысячной.

Существуют задачи, когда следовало бы найти приближенное значение определенного интеграла с необходимой точностью, тогда применяют численное интегрирование такое, как метод Симпосна, трапеций, прямоугольников. Не все случаи позволяют вычислить его с определенной точностью.

Данная статья рассматривает применение формулы Ньютона-Лейбница. Это необходимо для точного вычисления определенного интеграла. Будут приведены подробные примеры, рассмотрены замены переменной в определенном интеграле и найдем значения определенного интеграла при интегрировании по частям.

Формула Ньютона-Лейбница

Чтобы произвести доказательство этой формулы, необходимо использовать понятие интеграла с имеющимся переменным верхним пределом.

Когда функция y = f(x) непрерывна на отрезке [a; b], тогда значение аргумента x ∈ [a; b], а интеграл имеет вид ∫_a^xf(t)dt и считается функцией верхнего предела. Необходимо принять обозначение функции примет вид ∫_a^xf(t)dt = Φ(x), она является непрерывной, причем для нее справедливо неравенство вида ∫_a^xf(t)dt' = Φ'(x) = f(x).

Зафиксируем, что приращении функции Φ(x) соответствует приращению аргумента ∆x, необходимо воспользоваться пятым основным свойством определенного интеграла и получим

Φ(x+∆x)-Φ(x) = ∫_a^x+∆xf(t)dt - ∫_a^xf(t)dt = ∫_a^x+∆xf(t)dt = f(c)·(x+∆x)-x = f(c)·∆x,

где значение c ∈ x; x+∆x.

Зафиксируем равенство в виде Φ(x+∆x)-Φ(x)∆x = f(c). По определению производной функции необходимо переходить к пределу при ∆x→0, тогда получаем формулу вида Φ'(x) = f(x). Получаем, что Φ(x) является одной из первообразных для функции вида y = f(x), расположенной на [a; b]. Иначе выражение можно записать

F(x) = Φ(x) + C = ∫_a^xf(t)dt + C, где значение C является постоянной.

Произведем вычисление F(a) с использованием первого свойства определенного интеграла. Тогда получаем, что

F(a) = Φ(a) + C = ∫_a^af(t)dt + C = 0 + C = C, отсюда получаем, что C = F(a). Результат применим при вычислении F(b) и получим:

F(b) = Φ(b) + C = ∫_a^bf(t)dt + C = ∫_a^bf(t)dt + F(a), иначе говоря, F(b) = ∫_a^bf(t)dt + F(a). Равенство доказывает формулу Ньютона-Лейбница ∫_a^bf(x)dx + F(b) - F(a).

Приращение функции принимаем как F_ab = F(b) - F(a). С помощью обозначения формула Ньютона-Лейбница принимает вид ∫_a^bf(x)dx = F_ab = F(b) - F(a).

Чтобы применить формулу, обязательно необходимо знать одну из первообразных y = F(x) подынтегральной функции y = f(x) из отрезка [a; b].