Что такое признаки делимости на 10 на 5 и на 2?

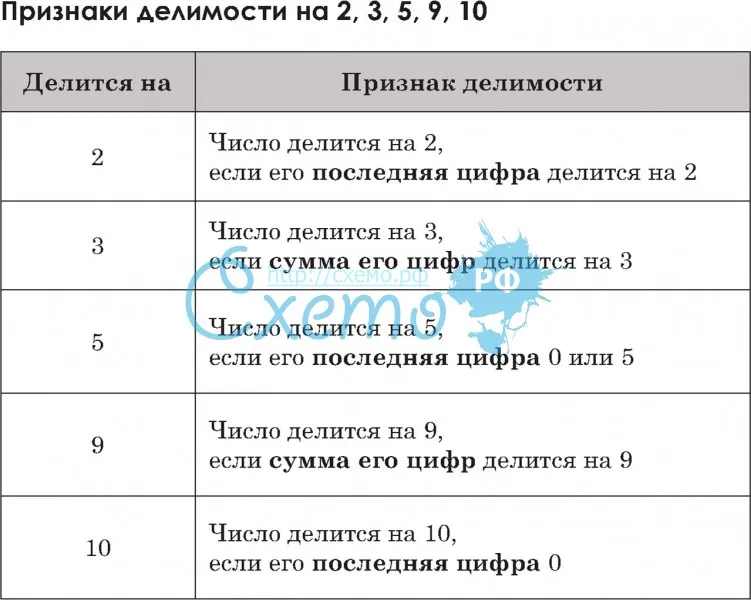
Узнайте, что такое признаки делимости на 10 на 5 и на 2 и как они могут помочь в быстром определении, делится ли число на 10, на 5 или на 2. Признаки делимости являются важным инструментом в математике, упрощающим решение арифметических задач. Читайте статью на NOCFN.

Деление чисел издавна считалось задачей куда более трудной, чем умножение. Поэтому делить люди научились гораздо позже, чем умножать. Учёные-математики долго занимались поиском наиболее простого способа деления чисел. Данный способ называется деление «уголком», такой способ деления используем в математике, который впервые появился в Европе в 10 веке и получил название «золотое деление». Но на такой способ деление уголком обычно затрачивается много времени, а могут возникать ситуации, когда нужно быстро определить, делится одно число на другое или нет. В этом помогают простые, легко запоминающиеся признаки.

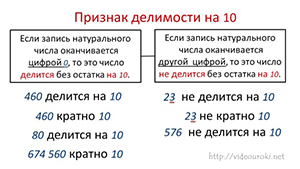
Признак делимости на 10

Всякое натуральное число, запись которого оканчивается цифрой 0, делится без остатка на 10. Чтобы получить частное, достаточно отбросить цифру 0. Например, 280 делится без остатка на 10, так как 280:10 = 28.

А при делении числа 283 на 10 получаем неполное частное 28 и остаток 3. Если последняя цифра в записи натурального числа отлична от нуля, то это число не делится без остатка на 10.

Вывод: если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10. Если запись натурального числа оканчивается другой цифрой, то оно не делится без остатка на 10.

Остаток в этом случае равен последней цифре числа.

Признак делимости на 5

Число 10 – это произведение 2*5. Число 10 делится без остатка на 2 и на 5. Отсюда и любое число, запись которого оканчивается цифрой 0, делится без остатка на 5 и на 2.

Например,

60:5 = 12;

60:2 = 30.

Вывод: если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5. Если же запись числа оканчивается иной цифрой, то число без остатка на 5 не делится.

Например, числа 870 и 875 делятся без остатка на 5, а числа 872 и 873 на 5 без остатка не делятся.

Признак делимости на 2

Числа, делящиеся без остатка на 2, называют четными, а числа, которые при делении на 2 дают остаток 1, называют нечетными. Из однозначных чисел четными числами являются: 0, 2, 4, 6, 8, а цифры 1, 3, 5, 7, 9 – нечетные. Все полные десятки делятся на 2 без остатка (они четны). Таким образом, любое натуральное число четно лишь тогда, когда в разряде единиц стоит четная цифра, и нечетна, когда в разряде единиц стоит нечетная цифра.

Вывод: если запись натурального числа оканчивается четной цифрой, то это число четно (делится без остатка на 2), а если запись числа оканчивается нечетной цифрой, то это число нечетно.

Например, числа 2, 60, 84, 96, 308 – четные, а числа 3, 51, 85, 97 – нечетные.

Признаки делимости на 10, на 5 и на 2

Известно, что любое натуральное число \(a\) можно представить в виде суммы некоторого числа десятков и однозначного числа.

Например:

• 37=3⋅10+7;
• 124=12⋅10+4;
• 6782=678⋅10+2.

В общем виде можно записать так:

a=m⋅10+n, где

• \(n\) — это последняя цифра в записи числа \(a\).

Первое слагаемое, т. е. выражение m⋅10, делится и на \(2\), и на \(5\), и на \(10\), т. к. множитель \(10\) в этом произведении делится на каждое из названных чисел.

Поэтому делимость числа \(a\) на \(2\), на \(5\) или на \(10\) зависит от последней цифры числа \(a\), т. е. от цифры \(n\).

Также можно сформулировать признак делимости на \(4\):

Если две последние цифры числа \(a\) образуют число, делящееся на \(4\), то само число \(a\) делится на \(4\).

Вывод: признаки делимости на 10, на 5 и на 2 позволяют быстро определить, делится ли число на 10, на 5 или на 2, исходя из последней цифры числа.

Использование этих признаков помогает упростить и ускорить решение арифметических задач.

Понятие признаков делимости чисел

Признаки делимости чисел - это особенности чисел, которые помогают быстро определить, делится ли данное число на другое. Знание этих признаков необходимо при решении многих арифметических задач.

Признак делимости на 10

Рассмотрим несколько чисел, запись которых оканчивается цифрой 0, например,

• 60,
• 130,
• 2340.

Каждое из этих чисел делится без остатка на 10.

Чтобы получить частное, достаточно отбросить цифру 0.

Например, 60 : 10 = 6, 130 : 10 = 13, 2340 : 10 = 234.

Вывод: любое натуральное число, запись которого оканчивается цифрой 0, делится без остатка на 10.

Если последняя цифра в записи натурального числа отлична от нуля, то это число не делится без остатка на 10.

Проверим это утверждение, например, на числе 234.

234 : 10 = 23 целых в остатке 4 (неполное частное 23 и остаток 4 - последняя цифра в записи числа 234).

Вывод: если последняя цифра в записи натурального числа отлична от нуля, то это число не делится без остатка на 10.

Определение:

Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10.

Если запись натурального числа оканчи­вается другой цифрой, то оно не делится без остатка на 10.

Остаток в этом случае равен последней цифре в записи числа.

Обратим внимание на то, что число 10 = 2 · 5 (число 10 делится без остатка и на 2, и на 5).

Вывод: число, запись которого оканчивается цифрой 0, делится без остатка и на 5, и на 2.

Например, 70 = 7 · 10 = 7 · (2 · 5) = (7 · 2) · 5 = 14 · 5, значит, 70 : 5 = 14.

А из того что 70 = 7 · (5 · 2) = (7 · 5) · 2 = 35 · 2, получаем, что 70 : 2 = 35.

Полные десятки

Существует такое понятие, как "круглое" число - это целое число, запись которого оканчивается одним или несколькими нулями. Такие числа принято называть "круглыми" ("полными") десятками.

Например, числа 40, 530, 3270, 3200 являются полными десятками.

40 - четыре десятка

530 - пятьдесят три десятка

3270 - триста двадцать семь десятков

3200 - триста двадцать десятков

Полные десятки делятся и на 10, и на 5, и на 2.

Признак делимости на 5

Каждое число можно представить в виде суммы полных десятков и еди­ниц, например, 

46 = 40 + 6, 539 = 530 + 9, 3278 = 3270 + 8.

Так как полные десятки делятся на 5, то и всё число делится на 5 лишь в том случае, когда на 5 делится число единиц.

Это возможно только тогда, когда в разряде единиц стоит цифра 0 или 5.

Определение:

Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5.

Если запись натурального числа оканчивается другой цифрой, то оно не делится без остатка на 5.

Признак делимости на 2

Числа, делящиеся без остатка на 2, называют четными, а числа, которые при делении на 2 дают остаток 1, называют нечетными. Из однозначных чисел четными числами являются: 0, 2, 4, 6, 8, а цифры 1, 3, 5, 7, 9 – нечетные. Все полные десятки делятся на 2 без остатка (они четны). Таким образом, любое натуральное число четно лишь тогда, когда в разряде единиц стоит четная цифра, и нечетна, когда в разряде единиц стоит нечетная цифра.

Определение:

Если запись натурального числа оканчивается четной цифрой, то это число четно (делится без остатка на 2), а если запись числа оканчивается нечетной цифрой, то это число нечетно.

Признаки делимости на 10, на 5 и на 2

Известно, что любое натуральное число \(a\) можно представить в виде суммы некоторого числа десятков и однозначного числа.

Например:

• 37=3⋅10+7;
• 124=12⋅10+4;
• 6782=678⋅10+2.

В общем виде можно записать так:

a=m⋅10+n, где

• \(n\) — это последняя цифра в записи числа \(a\).

Первое слагаемое, т. е. выражение m⋅10, делится и на \(2\), и на \(5\), и на \(10\), т. к. множитель \(10\) в этом произведении делится на каждое из названных чисел.

Поэтому делимость числа \(a\) на \(2\), на \(5\) или на \(10\) зависит от последней цифры числа \(a\), т. е. от цифры \(n\).

Также можно сформулировать признак делимости на \(4\):

Если две последние цифры числа \(a\) образуют число, делящееся на \(4\), то само число \(a\) делится на \(4\).

Вывод: признаки делимости на 10, на 5 и на 2 позволяют быстро определить, делится ли число на 10, на 5 или на 2, исходя из последней цифры числа.

Использование этих признаков помогает упростить и ускорить решение арифметических задач.

Признаки делимости в математике

Признаки делимости являются важным инструментом в математике для быстрого определения, делится ли одно число на другое. Эти признаки основаны на различных свойствах чисел и позволяют сделать выводы о делимости без необходимости выполнения самого деления.

Используя признаки делимости на 10, на 5 и на 2, мы можем быстро и легко определить, делится ли число на 10, на 5 или на 2, исходя из его последней цифры.

Например, если число оканчивается цифрой 0, то оно делится на 10 без остатка. Если число оканчивается цифрой 5 или 0, то оно делится на 5 без остатка. Если число оканчивается четной цифрой (0, 2, 4, 6, 8), то оно делится на 2 без остатка.

Признаки делимости на 10, на 5 и на 2 являются простыми и полезными инструментами для быстрого решения различных математических задач. Их знание позволяет существенно упростить и ускорить процесс работы с числами и делать более точные выводы о свойствах чисел.

В заключение можно сказать, что признаки делимости на 10, на 5 и на 2 являются важными инструментами в математике, которые помогают быстро и легко определить, делится ли число на другое без необходимости выполнения самого деления. Их использование позволяет упростить и ускорить решение различных арифметических задач.

Что нам скажет Википедия?

При́знак дели́мости — алгоритм, позволяющий сравнительно быстро определить, является ли число кратным заранее заданному. Если признак делимости позволяет выяснить не только делимость числа на заранее заданное, но и остаток от деления, то его называют признаком равноостаточности.

Как правило, признаки делимости применяются при ручном счёте и для чисел, представленных в конкретной позиционной системе счисления (обычно десятичной).

Понятия делимости, равноделимости и равноостаточности

Основные статьи: Делимость и Равноостаточность

Если для двух целых чисел $a$ и $b$ существует такое целое число $q,$ что

$a\; =\; bq$

$(1)$

то говорят, что число $a$ делится на $b.$

Два целых числа $a$ и $b$ называются равноделимыми на $m,$ если либо они оба делятся на $m,$ либо оба не делятся.

Два целых числа $a$ и $b$ равноостаточны при делении на натуральное число $m$ (или сравнимы по модулю $m$), если при делении на $m$ они дают одинаковые остатки, то есть существует такие целые числа $q\_\{1\},\backslash ,q\_\{2\},\backslash ,r,$ что

$a\; =\; mq\_\{1\}\; +\; r$	$(2)$
$b\; =\; mq\_\{2\}\; +\; r$	$(3)$

Общие принципы построения

Пусть требуется определить, делится ли некоторое натуральное число $A$ на другое натуральное число $m.$ Для этого возьмём последовательность натуральных чисел:

$A,m,m^2,m^3,\backslash dots,m^n$

такую, что:

Тогда, если последний член этой последовательности равен нулю, то $A$ делится на $m,$ в противном случае $A$ на $m$ не делится.

Способ (алгоритм) построения такой последовательности и будет искомым признаком делимости на $m.$ Математически он может быть описан с помощью функции $f(x),$ определяющей каждый следующий член последовательности в зависимости от предыдущего:

$f(x)\; =\; mx,\backslash quad\; x\backslash in\backslash mathbb\{N\},$

удовлетворяющей следующим условиям:

1. $f(0)\; =\; m^0\; =\; 1,$
2. $f(1)\; =\; mf(0)\; =\; m^1,$
3. $f(2)\; =\; mf(1)\; =\; m^2,$
4. и т.д.

Если требование равноделимости для всех членов последовательности заменить на более строгое требование равноостаточности, то последний член этой последовательности будет являться остатком от деления $A$ на $m,$ а способ (алгоритм) построения такой последовательности будет признаком равноостаточности на $m.$ В силу того, что из равенства остатка при делении на $m$ нулю следует делимость на $m$, любой признак равноостаточности может применяться как признак делимости. Математически признак равноостаточности тоже может быть описан с помощью функции $f(x),$ определяющей каждый следующий член последовательности в зависимости от предыдущего:

$f(x)\; =\; mx,\backslash quad\; x\backslash in\backslash mathbb\{N\},$

удовлетворяющей следующим условиям:

1. $f(0)\; =\; m^0\; =\; 1,$
2. $f(1)\; =\; mf(0)\; =\; m^1,$
3. $f(2)\; =\; mf(1)\; =\; m^2,$
4. и т.д.

Примером такой функции, определяющей признак равноостаточности (и, соответственно, признак делимости), может быть функция

$f(x)\; =\; 10x,$

а последовательность, построенная с её помощью будет иметь вид:

$10,\; 100,\; 1000,\; 10000,\; \backslash dots$

По сути применение признака равноостаточности на базе этой функции эквивалентно делению при помощи вычитания.

Другим примером может служить общеизвестный признак делимости (а также равноостаточности) на 10.

Математически этот признак равноостаточности может быть сформулирован следующим образом. Пусть надо выяснить остаток от деления на 10 натурального числа $A,$ представленного в виде

$A\; =\; a\_0\; \backslash cdot\; 10^0\; +\; a\_1\; \backslash cdot\; 10^1\; +\; \backslash dots\; +\; a\_n\; \backslash cdot\; 10^n,$

Тогда остатком от деления $A$ на 10 будет $a\_0.$ Функция, описывающая этот признак равноостаточности будет выглядеть как

$f(x)\; =\; 10^x,\backslash quad\; x\backslash in\backslash mathbb\{N\},$

Легко доказать, что эта функция удовлетворяет всем перечисленным выше требованиям. Причём последовательность, построенная с её помощью, будет содержать всего один или два члена.

Также легко видеть, что такой признак ориентирован именно на десятичное представление числа $A$ — так, например, если применять его на компьютере, использующем двоичную запись числа, то чтобы выяснить $a\_0,$ программе пришлось бы сначала поделить $A$ на 10.

Для построения признаков равноостаточности и делимости чаще всего используется следующие теоремы:

Признаки делимости в десятичной системе счисления

Признак делимости на 2

Число делится на 2 тогда и только тогда, когда его последняя цифра делится на 2, то есть является чётной.

Соответствующая признаку функция (см. раздел «Общие принципы построения»):

$f(x)\; =\; 2x,$

Эта функция помимо признака делимости задаёт и признак равноостаточности.

Признак делимости на 3

Число делится на 3, когда сумма его цифр делится на 3. Например, число 159 делится на 3, поскольку сумма его цифр 1 + 5 + 9 = 15 делится на 3.

Соответствующая признаку функция:

$f(x)\; =\; x\_0\; +\; x\_1\; +\; \backslash dots\; +\; x\_n,\backslash quad\; x\_i\; -\; \backslash text\{i-я\; цифра\; числа\; \}\; A\; \backslash text\{\; в\; позиционной\; системе\; счисления\},$

Эта функция помимо признака делимости задаёт и признак равноостаточности. Например, числа 154, 1 + 5 + 4 = 10 и 1 + 0 = 1 равноостаточны при делении на 3.

Признак делимости на 4

Число делится на 4, когда две последние цифры нули или составляют число, делящееся на 4. Например, 14676 — последние цифры 76, и число 76 делится на 4: 76:4=19. Двузначное число делится на 4 тогда и только тогда, когда удвоенная цифра в разряде десятков, сложенная с цифрой в разряде единиц, делится на 4. Например, число 42 не делится на 4, так как 2 ⋅ 4 + 2 = 10 не делится на 4.

Соответствующая признаку функция:

$f(x)\; =\; 2\; \backslash cdot\; x\_0\; +\; x\_1,\backslash quad\; x\_i\; -\; \backslash text\{i-я\; цифра\; числа\; \}\; A\; \backslash text\{\; в\; позиционной\; системе\; счисления\},$

Эта функция помимо признака делимости задаёт и признак равноостаточности. Например, числа 87, 8 ⋅ 2 + 7 = 23 и 2 ⋅ 2 + 3 = 7 равноостаточны при делении на 4.

Более простая формулировка: Число делится на 4, если в последнем разряде 0, 4, 8, а предпоследний разряд чётный; или если в последнем разряде 2, 6, а предпоследний разряд нечётный.

Признак делимости на 5

Число делится на 5 тогда и только тогда, когда оно оканчивается на 0 или на 5.

Соответствующая признаку функция:

$f(x)\; =\; x\_0,\backslash quad\; x\_i\; -\; \backslash text\{i-я\; цифра\; числа\; \}\; A\; \backslash text\{\; в\; позиционной\; системе\; счисления\},$

Эта функция помимо признака делимости задаёт и признак равноостаточности.

Признак делимости на 6

Число делится на 6 тогда и только тогда, когда оно делится и на 2, и на 3 (то есть если оно чётное и сумма его цифр делится на 3).

Другой признак делимости: число делится на 6 тогда и только тогда, когда учетверённое число десятков, сложенное с цифрой в разряде единиц, делится на 6.

Соответствующая признаку функция:

$f(x)\; =\; 2\; \backslash cdot\; x\_0\; +\; x\_1,\backslash quad\; x\_i\; -\; \backslash text\{i-я\; цифра\; числа\; \}\; A\; \backslash text\{\; в\; позиционной\; системе\; счисления\},$

Эта функция помимо признака делимости задаёт и признак равноостаточности. Например, числа 73, 7 ⋅ 4 + 3 = 31, 3 ⋅ 4 + 1 = 13 и 1 ⋅ 4 + 3 = 7 равноостаточны при делении на 6.

Признак делимости на 7

Признак 1:

число делится на 7 тогда, когда утроенное число десятков, сложенное с цифрой в разряде единиц, делится на 7. Например, 154 делится на 7, так как на 7 делится 15 ⋅ 3 + 4 = 49. 1001 делится на 7, так как на 7 делятся 100 ⋅ 3 + 1 = 301, 30 ⋅ 3 + 1 = 91, 9 ⋅ 3 + 1 = 28